ChatGPT:
Playing with Reason: Lewis Carroll’s The Game of Logic
Lewis Carroll—mathematician, logician, and part-time Wonderland tour guide—didn’t just write about talking rabbits and disappearing cats. In 1886, he published The Game of Logic, a short book that aimed to teach reasoning through play. Imagine someone trying to explain algebra to you by handing you a board game instead of a headache—that’s basically what Carroll did.
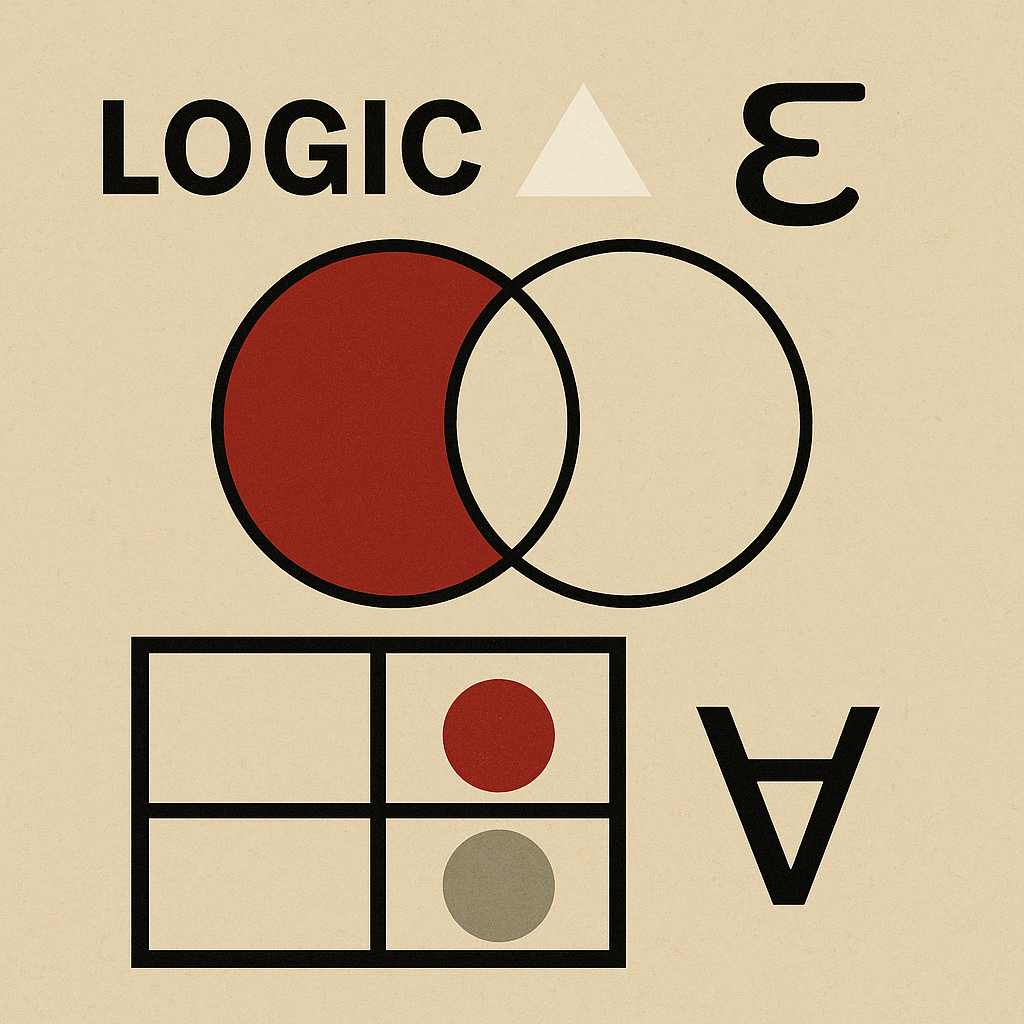
The book looks deceptively innocent. It comes with a game board divided into four squares, a handful of red and grey counters, and the promise that, by moving them around, you’ll learn to think logically. Of course, this being Carroll, “simple” quickly turns into “wait, what?” But underneath his Victorian whimsy lies something remarkably powerful: the early mechanics of modern logic and computer science.
What’s in the Game?
Carroll’s “board” represents all the possible ways two ideas can relate. For example, suppose we want to talk about cats and mammals (a safer topic than religion or politics). The board divides the universe into four neat zones:
- Cats that are mammals.
- Cats that are not mammals.
- Things that are not cats but are mammals.
- Things that are neither cats nor mammals.
Each little square represents one of these combinations. To communicate logical statements, Carroll used colored counters—red for “some exist,” and grey for “none exist.” It’s like turning abstract reasoning into a children’s counting game, but with more philosophical peril.
For instance:
- “All cats are mammals” means there are no cats that aren’t mammals, so you put a grey counter in zone 2.
- “Some cats are mammals” means there are some cats in the first zone, so that square gets a red counter.
- “No cats are mammals”? Grey counter in zone 1.
- “Some cats are not mammals”? Red counter in zone 2.
Each move on the board is actually performing what mathematicians now call a logical operation—a mix of intersection, complement, and union. If you’re feeling fancy, you can even write it in symbols, like ∃(A ∧ B), which means “there exists something that is both A and B.” But Carroll’s audience didn’t need symbols; they had counters, and possibly tea.
The Mathematical Magic Behind the Tea Party
From a modern mathematical perspective, Carroll was doing something radical: he was visualizing logic. Before symbolic logic took off in the early 20th century, reasoning was mostly done in words. Carroll, trained in mathematics, knew that words are slippery little creatures (he wrote Alice, after all). So he tried to make thought itself visible—spatial, mechanical, almost game-like.
That’s what makes The Game of Logic such an odd and brilliant artifact. It’s playful, but it’s not trivial. Beneath the cute surface is an early version of Boolean algebra—the same logic that would later form the basis of computer circuits, search engines, and the part of your phone that decides whether to send a message or die trying.
Carroll, of course, didn’t know he was inventing proto–computer science. He just wanted people to stop making bad arguments at dinner parties. But his logic game teaches exactly what modern mathematicians and programmers rely on: if you can express an idea clearly and consistently, you can manipulate it.
How Socrates Lost Again
Let’s take a classic logical chestnut:
All humans are mortal.
Socrates is a human.
Therefore, Socrates is mortal.
Using Carroll’s system, we set up two categories—Humans (A) and Mortal beings (B)—and one poor individual, Socrates (C). The statement “All humans are mortal” means there are no humans who aren’t mortal, so we put a grey counter in the part of the board representing “humans that are not mortal.” The statement “Socrates is a human” means our red counter representing Socrates goes in the “human” area.
Now, because the “non-mortal human” zone is greyed out (empty), every red counter in the “human” half automatically counts as “mortal” too. The conclusion follows automatically—Socrates can’t escape his fate.
Mathematically, that’s just:
A \subseteq B,\; C \in A \Rightarrow C \in B
Or, in English:
If all humans are mortal, and Socrates is human, then Socrates is mortal.
In Carroll’s world, logic isn’t lofty or mysterious—it’s just good housekeeping for ideas.
From Tea Tables to Truth Tables
The funniest part about The Game of Logic is that it predates the formal development of symbolic logic by only a few decades. Carroll was using toys and diagrams to do what logicians like Gottlob Frege and George Boole were turning into the serious machinery of mathematics.
If you’ve ever written a line of computer code like:

—congratulations, you’ve played The Game of Logic. You just used the same structure, only with fewer waistcoats.
Carroll’s version isn’t about computers, of course—it’s about thinking clearly. His game helps you see when a statement actually follows from another and when it’s just nonsense disguised as wisdom. If he were alive today, he’d probably be yelling at social media posts and muttering, “You’ve got a red counter where a grey one should be.”
Why It Still Matters
You don’t have to be a mathematician—or a Victorian—to appreciate what Carroll was doing. His game shows that logic is not cold or abstract; it’s the art of making sense. In an age drowning in half-truths, The Game of Logic is like a reminder from the 1880s that clarity is not optional.
Also, it’s fun. It’s the rare math book where you can actually play your way to understanding. By turning arguments into little colored counters, Carroll makes logic something you can literally hold in your hand.
So, next time you hear someone making a sweeping claim (“All politicians are honest,” for example), imagine Carroll’s board in your head. Which squares would the counters go in? Would there even be room for a red one?
That’s the quiet genius of The Game of Logic: it teaches you to think before you nod.
In short:
Carroll turned logic from a dusty discipline into a parlor game—and accidentally built a bridge to modern mathematics. It’s proof that reason, when presented with charm and a little sarcasm, can actually be delightful.
And if you’re ever tempted to say something illogical, just remember: somewhere, Lewis Carroll’s ghost is placing a grey counter on your behalf.
