ChatGPT:
Introducing Fractal Dimension: Its Origin and History
Understanding Fractals
A fractal is a complex geometric shape that exhibits self-similarity across different scales. This means that zooming into a small portion of the fractal reveals a structure similar to the whole. Fractals are characterized by intricate patterns that repeat indefinitely, making them infinitely complex.
What is Fractal Dimension?
Traditional geometric shapes are described using integer dimensions:
• A line is one-dimensional (1D).
• A plane or square is two-dimensional (2D).
• A cube is three-dimensional (3D).
However, fractals often require a non-integer, or fractional, dimension to describe their complexity adequately. This is where the concept of fractal dimension comes into play. The fractal dimension quantifies how completely a fractal appears to fill space as you zoom in, providing a statistical index of complexity comparing how detail in a pattern changes with the scale at which it is measured.
Origins of the Concept
• Early Mathematical Explorations
The roots of fractal dimensions trace back to the late 19th and early 20th centuries, when mathematicians began studying pathological curves and sets that defied traditional geometric intuition.
• Georg Cantor (1845–1918): Introduced the Cantor set, a simple yet paradoxical example demonstrating that a set can be uncountably infinite yet have zero measure.
• Helge von Koch (1870–1924): Created the Koch snowflake, a curve of infinite length that encloses a finite area, challenging conventional notions of dimension and measurement.
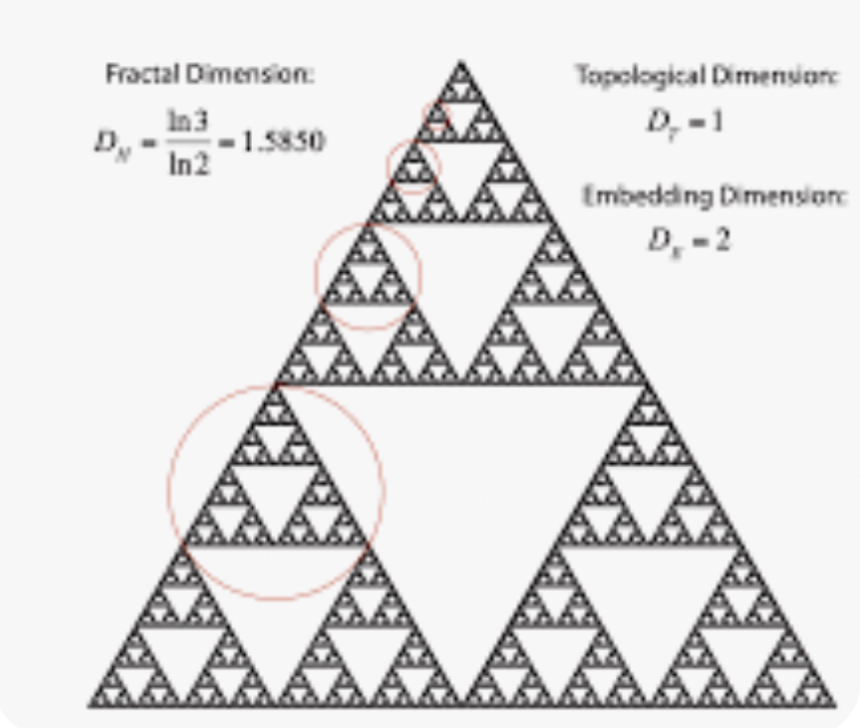
• Wacław Sierpiński (1882–1969): Developed the Sierpiński triangle and Sierpiński carpet, fractal shapes that exhibit self-similarity and fractional dimensions.
• Felix Hausdorff (1868–1942):
In 1918, Hausdorff introduced the concept of the Hausdorff dimension, a method to assign a fractional dimension to sets that are too “irregular” for traditional dimensions. This mathematical framework laid the groundwork for quantifying the complexity of fractals.
Benoit Mandelbrot and the Term ‘Fractal’
• Coining the Term:
The term fractal was coined by mathematician Benoit B. Mandelbrot in 1975, derived from the Latin word fractus, meaning “broken” or “fractured.”
• Mandelbrot’s Contributions:
Mandelbrot’s work was pivotal in bringing fractals into mainstream mathematics and science. In his seminal 1982 book, The Fractal Geometry of Nature, he demonstrated how fractals can model complex, irregular patterns found in nature, such as coastlines, clouds, and mountain ranges.
Development of Fractal Dimension
• Hausdorff Dimension:
The Hausdorff dimension is a mathematical concept that generalizes the notion of dimension to non-integer values. It is defined using measure theory and provides a way to quantify the size of a fractal set in terms of how it scales.
• Box-Counting Dimension (Minkowski–Bouligand Dimension):
A more computationally accessible method, the box-counting dimension involves covering the fractal with boxes of a certain size and analyzing how the number of boxes scales as the size changes. This method is widely used in practical applications due to its simplicity.
Historical Impact and Applications
• Mathematics and Physics:
The concept of fractal dimensions bridged gaps between pure mathematics and physical phenomena. It allowed for the description and analysis of irregular shapes and patterns that couldn’t be explained by classical geometry.
• Natural Phenomena:
Fractals and their dimensions have been instrumental in modeling natural structures and patterns, such as:
• Geography: Coastlines, mountain ranges, and river networks.
• Biology: Blood vessels, neuron structures, and plant growth patterns.
• Meteorology: Cloud formations and turbulence.
• Technology and Science:
Fractal dimensions are used in various fields, including:
• Computer Graphics: Generating realistic textures and landscapes.
• Signal Processing: Analyzing complex signals and time series.
• Medicine: Understanding patterns in medical imaging and pathology.
Modern Developments
With advancements in computing power, fractals and fractal dimensions have become essential tools in modern science and engineering. They are used in:
• Chaos Theory: Understanding dynamical systems that are highly sensitive to initial conditions.
• Fractal Antennas: Designing compact and efficient antennas for wireless communication.
• Financial Markets: Modeling stock market fluctuations and economic systems.
Conclusion
The fractal dimension is a fundamental concept that emerged from the need to describe and analyze complex, self-similar structures that traditional geometry couldn’t handle. From its early roots in mathematical curiosities to its formalization by Hausdorff and popularization by Mandelbrot, the fractal dimension has become a crucial tool in understanding the intricate patterns of the natural and technological world.
References
• Mandelbrot, B. B. (1982). The Fractal Geometry of Nature. W.H. Freeman and Company.
• Falconer, K. (2003). Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons.
Explaining the Role of Scaling in the Concept of Fractal Dimension
Introduction
Scaling is a fundamental concept in understanding fractals and their dimensions. In the context of fractal geometry, scaling refers to how a fractal’s pattern repeats at different sizes or magnifications. The fractal dimension quantifies this repetition by measuring how the detail or complexity of a fractal changes with scale. Essentially, scaling provides a bridge between the physical size of the fractal and its mathematical complexity.
Self-Similarity and Scaling
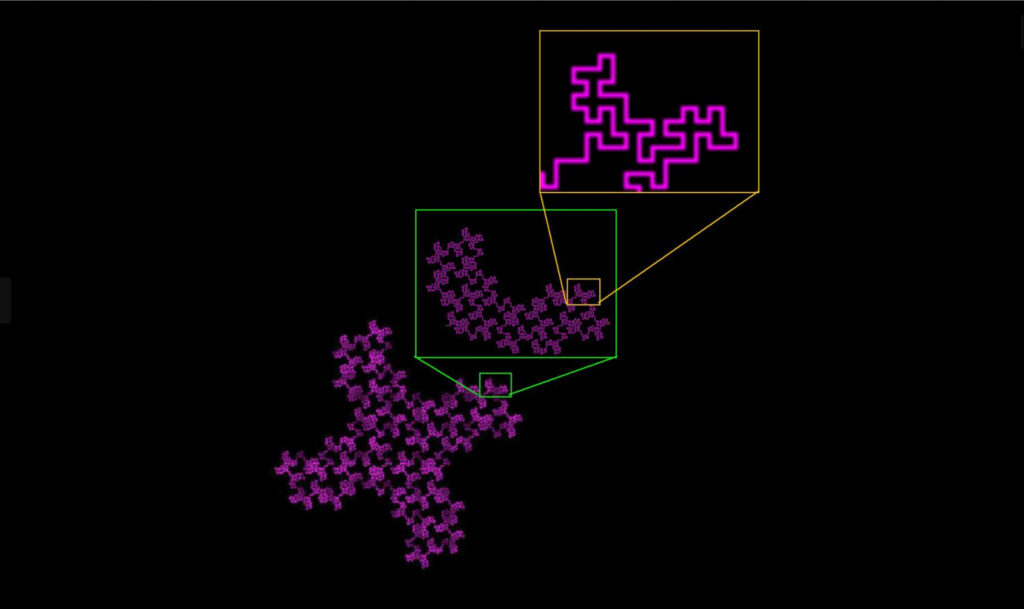
Fractals are often self-similar, meaning they look similar at any magnification. This property arises from scaling, where a fractal is composed of smaller copies of itself. When you zoom into a fractal, you see a repetition of the whole pattern on a smaller scale. This infinite repetition across scales is a key characteristic that distinguishes fractals from traditional geometric shapes.
Mathematical Role of Scaling in Fractal Dimension
The fractal dimension is mathematically defined using scaling relationships. It measures how the number of self-similar pieces (N) changes with the scaling factor (r). The basic formula connecting these quantities is:
Where:
• is the number of self-similar pieces.
• is the scaling factor (the ratio of the new size to the original size).
• is the fractal dimension.
Rearranged to solve for the fractal dimension:
This equation shows that the fractal dimension is directly related to how the number of pieces scales with size reduction.
Scaling in Different Dimensions
• One-Dimensional Objects (Lines): If you scale a line segment by a factor of , you need 2 copies to reconstruct the original line. Plugging into the formula:
• Two-Dimensional Objects (Squares): Scaling a square by requires 4 smaller squares to fill the original area:
• Fractals (Non-Integer Dimensions): For fractals, this relationship yields non-integer dimensions, reflecting their complexity.
Examples Illustrating the Role of Scaling
1. The Cantor Set:
• Construction: Start with a line segment (length 1). Remove the middle third. Repeat this process indefinitely for each remaining segment.
• Scaling Factor: Each segment is scaled by .
• Number of Pieces: At each iteration, the number of segments doubles ().
• Fractal Dimension:
• Interpretation: The Cantor set has a dimension less than 1, indicating it is more complex than a set of points but does not fill a line.
2. The Koch Snowflake:
• Construction: Begin with an equilateral triangle. For each side, add a smaller equilateral bump in the middle, scaling each segment by .
• Number of Pieces: Each iteration multiplies the number of sides by 4 ().
• Fractal Dimension:
• Interpretation: The Koch snowflake has a dimension between 1 and 2, reflecting its infinitely detailed curve that never becomes a plane.
Box-Counting Dimension and Scaling
The box-counting dimension is a practical method to estimate the fractal dimension, especially for complex or empirical data. It involves covering the fractal with boxes (or cubes in higher dimensions) of size and counting how the number of boxes changes as decreases.
The relationship is:
This formula highlights how scaling down the measurement units () affects the count of necessary elements to cover the fractal, revealing its dimension.
Scaling and Measure of Complexity
Scaling allows us to quantify the complexity or roughness of a fractal object. By observing how detail emerges at smaller scales, we understand how a fractal fills space differently from traditional geometric figures.
• Higher Fractal Dimension: Indicates that the fractal becomes increasingly complex as you zoom in, filling space more thoroughly.
• Lower Fractal Dimension: Suggests that the fractal is sparser, with less detail appearing at smaller scales.
Importance of Scaling in Natural Phenomena
Many natural patterns exhibit fractal-like scaling:
• Coastlines: The measured length increases as the measurement scale decreases, a phenomenon known as the “coastline paradox.”
• Vegetation Patterns: Branching patterns in trees and blood vessels show self-similar structures at different scales.
• Geological Formations: Mountain ranges and river networks display fractal characteristics, where scaling helps in modeling their complexity.
Scaling in Physical and Mathematical Contexts
• Renormalization Group Theory: In physics, scaling is crucial in understanding phase transitions and critical phenomena. It examines how physical systems behave similarly at different scales.
• Chaos Theory: Scaling laws help describe how small changes at microscopic levels can lead to significant differences at macroscopic levels.
Conclusion
Scaling is integral to the concept of fractal dimension because it captures how a fractal’s complexity changes with magnification. By analyzing the scaling behavior of fractals, we can assign a dimension that reflects their intricate patterns, bridging the gap between geometry and the irregular shapes found in nature. Scaling not only provides mathematical insight but also enhances our understanding of the underlying principles governing complex systems across various scientific fields.
References
• Falconer, K. (2003). Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons.
• Mandelbrot, B. B. (1982). The Fractal Geometry of Nature. W.H. Freeman and Company.
Explaining How Fractal Dimension Applies in Surface Science
Introduction
In surface science, understanding and characterizing surface morphology is crucial because the physical and chemical properties of materials are often significantly influenced by their surface structures. Traditional geometric measures may not adequately describe the complex, irregular features commonly observed on surfaces at microscopic and nanoscopic scales. This is where the concept of fractal dimension becomes valuable. The fractal dimension provides a quantitative measure of surface roughness and complexity, allowing scientists and engineers to analyze and predict surface behaviors more effectively.
Role of Fractal Dimension in Characterizing Surface Roughness
• Surface Complexity:
Surfaces often exhibit irregularities and roughness that are self-similar across different scales, a characteristic of fractal objects. The fractal dimension captures this self-similarity and complexity, offering a more comprehensive description than traditional Euclidean dimensions.
• Quantitative Measure of Roughness:
The fractal dimension serves as a numerical value representing the degree of surface roughness:
• Lower Fractal Dimension: Indicates a smoother surface with less complexity.
• Higher Fractal Dimension: Reflects a rougher surface with more intricate features.
• Comparison Across Scales:
Since fractal dimensions account for patterns at multiple scales, they enable the comparison of surface roughness regardless of the observation scale, which is essential for materials analyzed under varying magnifications.
Methods for Determining Fractal Dimensions of Surfaces
Several techniques are used to measure the fractal dimension of surfaces, primarily based on data obtained from surface imaging methods:
1. Atomic Force Microscopy (AFM):
• Provides high-resolution, three-dimensional surface topography.
• Allows for detailed analysis of surface features at the nanoscale.
• Fractal dimensions are calculated using the data from AFM scans.
2. Scanning Tunneling Microscopy (STM):
• Used for conductive surfaces, providing atomic-level surface details.
• Useful for analyzing electronic properties in relation to surface morphology.
3. Profilometry:
• Measures surface profiles and roughness over larger scales.
• Contact and non-contact profilometers can be used depending on the surface type.
4. Image Analysis Techniques:
• Box-Counting Method:
• The surface is overlaid with a grid of boxes of varying sizes.
• The number of boxes containing part of the surface profile is counted.
• The fractal dimension is calculated based on how this number changes with box size.
• Power Spectral Density (PSD) Analysis:
• Analyzes the frequency content of surface profiles.
• Relates the fractal dimension to the slope of the PSD curve in a log-log plot.
5. Mathematical Modeling:
• Models based on fractional Brownian motion can simulate and analyze surface roughness.
• Statistical methods are applied to correlate the models with experimental data.
Applications and Implications in Surface Science
1. Adhesion and Friction:
• Adhesion: Rougher surfaces (higher fractal dimensions) may exhibit increased adhesion due to greater contact area at microscopic levels.
• Friction: Surface roughness affects frictional forces between materials. Understanding fractal dimensions helps in designing surfaces with desired frictional properties.
2. Wettability and Coatings:
• Hydrophobicity/Hydrophilicity: Surface roughness influences how liquids spread on a surface.
• Coating Performance: The adherence and effectiveness of coatings depend on the underlying surface morphology.
3. Catalysis and Reactivity:
• Active Surface Area: Catalytic reactions often occur at surface sites; higher fractal dimensions can indicate more active sites.
• Reactivity: Surface roughness can affect adsorption energies and reaction kinetics.
4. Optical Properties:
• Scattering and Absorption: Surface roughness influences light interaction, affecting reflectivity and absorption.
• Anti-Reflective Surfaces: Designing surfaces with specific fractal dimensions can minimize unwanted reflections.
5. Mechanical Properties:
• Strength and Durability: Micro-scale surface features can impact fatigue resistance and material strength.
• Wear Resistance: Understanding surface roughness helps in predicting and enhancing wear properties.
6. Biomedical Applications:
• Implant Surfaces: Surface roughness affects cell adhesion and tissue integration in biomedical implants.
• Drug Delivery Systems: The morphology of carrier surfaces can influence drug release profiles.
Examples Illustrating the Application
1. Coating Adhesion:
• Paints and Protective Coatings: A surface with an optimal fractal dimension ensures better mechanical interlocking of the coating material, enhancing durability.
2. Semiconductor Industry:
• Wafer Surface Preparation: The electronic properties of semiconductor devices are sensitive to surface morphology. Controlling fractal dimensions during polishing processes improves device performance.
3. Anti-Icing Surfaces:
• Aircraft Wings: Surfaces designed with specific roughness profiles prevent ice accumulation by minimizing adhesion sites, relying on fractal analysis to optimize textures.
4. Oil Recovery:
• Porous Rocks: The fractal nature of pore surfaces in reservoir rocks affects fluid flow and extraction efficiency. Understanding fractal dimensions aids in modeling and improving recovery methods.
5. Textile Engineering:
• Fabric Surface Treatment: Modifying the surface roughness of fibers can alter fabric properties like breathability and moisture wicking, tailored through fractal dimension analysis.
Implications for Research and Development
• Material Design:
Fractal dimension analysis assists in tailoring materials with specific surface properties for targeted applications, from superhydrophobic surfaces to high-friction interfaces.
• Quality Control:
In manufacturing, monitoring the fractal dimensions of surfaces ensures consistency and performance, crucial for industries like aerospace and electronics.
• Predictive Modeling:
Incorporating fractal dimensions into models improves the prediction of surface-related phenomena, enhancing simulation accuracy for research and development.
Conclusion
The fractal dimension is a powerful tool in surface science, providing a quantitative measure of surface roughness and complexity that traditional geometry cannot offer. By capturing the self-similar and scale-invariant properties of surfaces, fractal dimension analysis enables a deeper understanding of how surface morphology influences material properties and behaviors. This understanding is vital for designing and optimizing materials across various industries, including electronics, biotechnology, materials engineering, and more. As imaging technologies and computational methods continue to advance, the application of fractal dimensions in surface science is likely to expand, offering even more insights into the intricate world of material surfaces.
References
• Majumdar, A., & Bhushan, B. (1990). Fractal model of elastic-plastic contact between rough surfaces. Journal of Tribology, 112(2), 205-216.
• Thomas, T. R. (1999). Rough Surfaces. Imperial College Press.
• Bennet, J. M., & Mattsson, L. (1999). Introduction to Surface Roughness and Scattering. Optical Society of America.
• Tong, Q. Y., & Gösele, U. (1999). Semiconductor Wafer Bonding: Science and Technology. Wiley-Interscience.
• Bigerelle, M., & Anselme, K. (2005). Statistical correlation between cell adhesion and proliferation on biocompatible metallic materials. Journal of Biomedical Materials Research Part A, 72A(1), 36-46.
How the Theory of Fractal Dimensions Applies in Scientific Fields
1. Physics and Material Science:
Fractal dimensions help describe surfaces and interfaces that are too complex or irregular for traditional Euclidean measures. For instance, analyzing the fractal dimension of a metal surface can yield insights into its roughness, affecting properties like friction, adhesion, and wear. In materials science, this understanding leads to improved surface coatings, better mechanical performance, and the engineering of surfaces with specific optical or electrical characteristics.
2. Geology and Earth Sciences:
Many geological formations—coastlines, mountain ranges, river networks—exhibit fractal patterns. Measuring their fractal dimensions enables scientists to model these natural structures more accurately, predict erosion patterns, understand seismic activity distributions, and assess the complexity of porous rock formations for better resource extraction strategies.
3. Biology and Medicine:
Biological structures often follow fractal principles. Blood vessels, bronchial tubes, and neural networks have branching patterns that can be described using fractal dimensions. In medicine, quantifying the complexity of these patterns assists in diagnosing diseases that alter the vascular network’s geometry, developing more efficient drug delivery systems, and understanding tissue growth and morphology.
4. Ecology and Environmental Science:
Fractal dimension measurements help ecologists characterize spatial distributions of vegetation, animal habitats, and soil aggregates. Analyzing these patterns can guide conservation efforts, predict species dispersal, and model ecosystem dynamics more accurately, especially under environmental stressors like climate change.
5. Meteorology and Climate Science:
Cloud formations, turbulence, and weather patterns have fractal-like properties. Fractal dimensions enable meteorologists and climate scientists to model cloud dispersion, analyze the complexity of air currents, and improve understanding of atmospheric turbulence. Such insights can enhance weather prediction models and contribute to studies on climate variability and change.
6. Computer Science and Image Analysis:
In computer graphics, fractal dimensions help generate naturalistic landscapes, textures, and patterns with minimal data input. In image processing, fractal analysis can classify textures, detect anomalies in medical images, and compress complex images efficiently.
7. Economics and Finance:
Though more abstract, the fluctuations in stock prices and market indices have been studied using fractal concepts. By assigning fractal dimensions to financial time series, analysts attempt to characterize market volatility, identify patterns in trading behavior, and develop more robust risk assessment models.
In essence, fractal dimension theory provides a powerful mathematical tool to quantify and understand the complexity inherent in irregular, natural, and man-made systems across numerous scientific disciplines.

