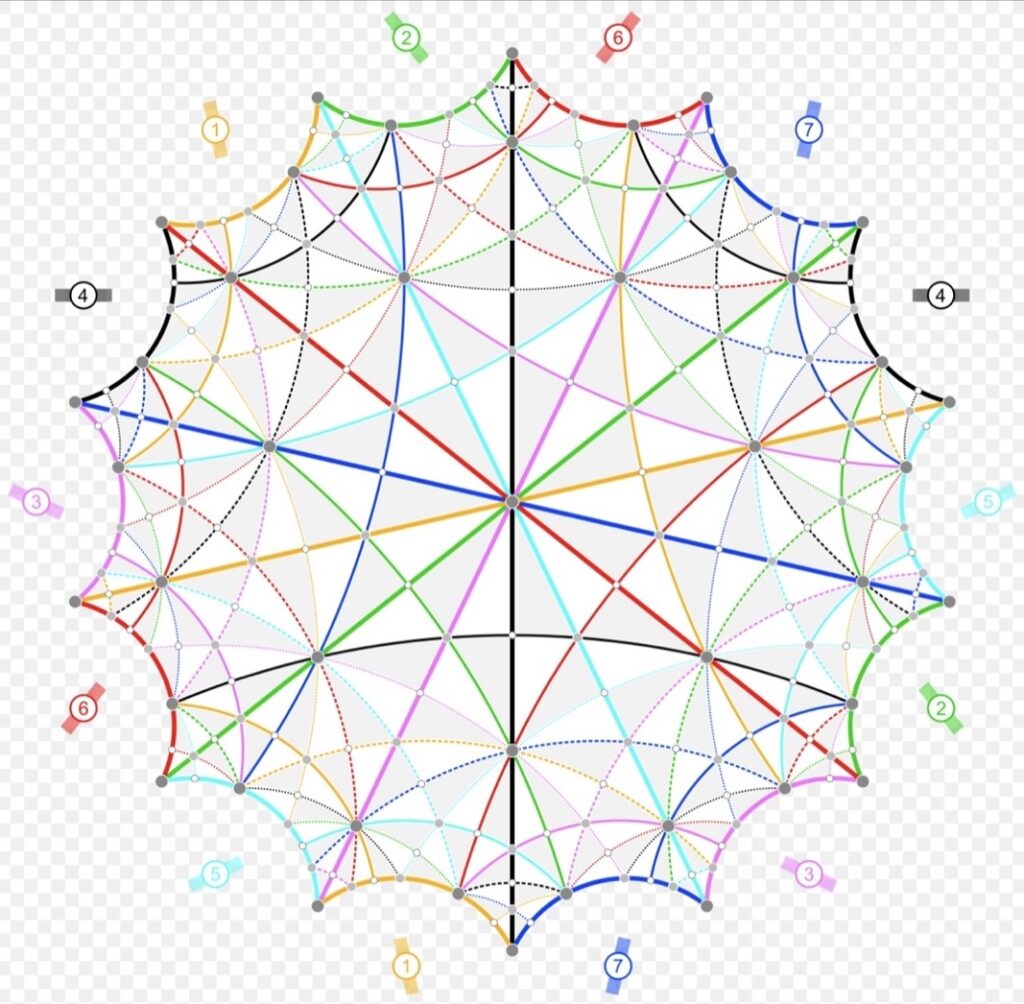
ChatGPT:The image depicts a representation of the Klein quartic, a complex algebraic curve of significant interest in various areas of mathematics, including algebraic geometry, number theory, and hyperbolic geometry.
Here’s a breakdown of the key elements:
- Klein Quartic: This is a specific type of Riemann surface that has a high degree of symmetry. It’s defined by a particular algebraic equation in complex projective space.
- Geodesics: The image shows 28 geodesics on the Klein quartic. A geodesic is the shortest path between two points on a surface.
- Color Coding and Patterns: The geodesics are marked by 7 colors and 4 patterns. This is likely to illustrate different families of geodesics or different types of symmetry within the Klein quartic. Each color and pattern combination represents a unique geodesic path or symmetry.
- Hyperbolic Geometry: The shape of the Klein quartic is consistent with hyperbolic geometry, which is a non-Euclidean geometry where the parallel postulate does not hold. The wavy, almost fractal-like boundary is a typical feature of hyperbolic surfaces.
- Symmetry: The diagram emphasizes the high degree of symmetry in the Klein quartic. The regular arrangement of colors and patterns shows that the surface can be divided into symmetrical parts.
In summary, this image is a highly structured and symmetrical representation of the Klein quartic, highlighting the complex interplay of geodesics and symmetries in hyperbolic geometry.
Klein Quartic: Overview
The Klein quartic is a highly symmetric algebraic curve or Riemann surface defined by the equation:
[ x^3y + y^3z + z^3x = 0 ]
Origin
- Felix Klein: The curve is named after the German mathematician Felix Klein, who studied its properties in the late 19th century.
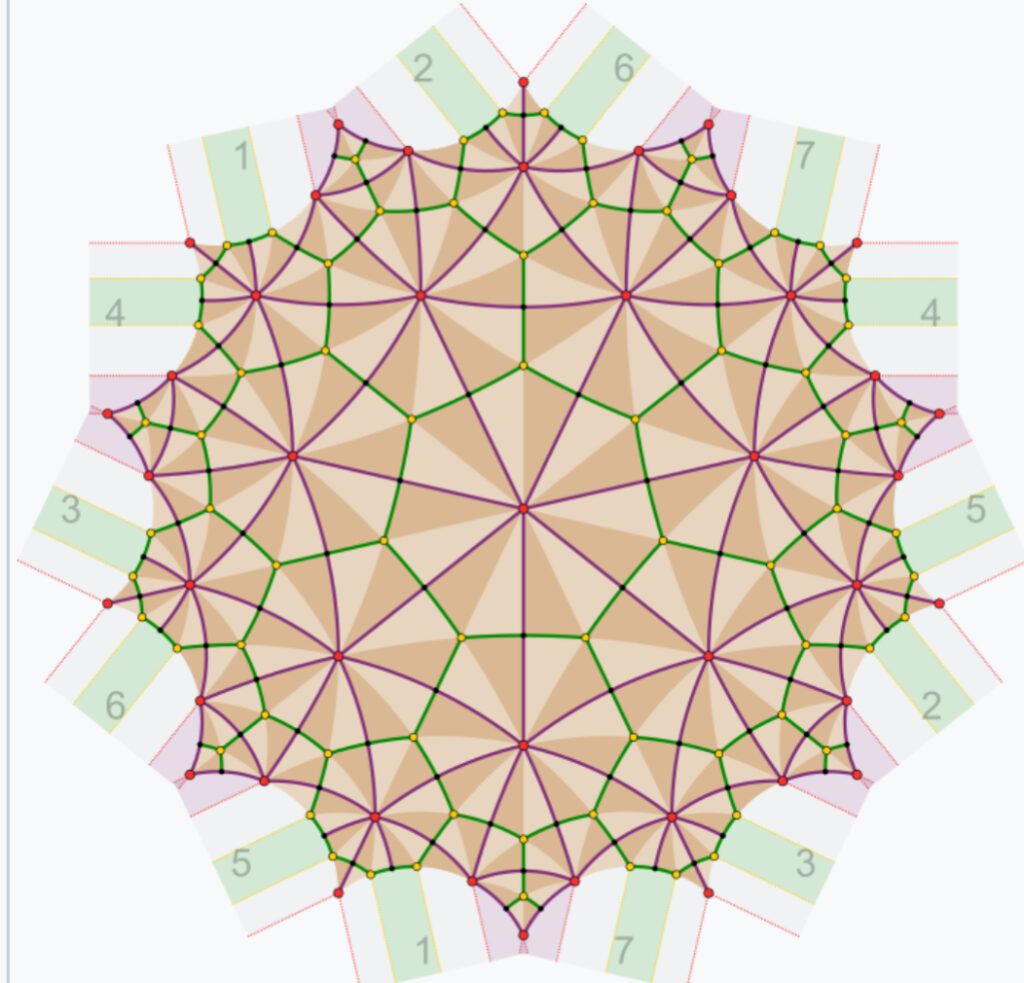
- Discovery: Klein discovered that this curve, which lies in the projective plane, has a genus of 3 and possesses a high degree of symmetry.
Mathematical Significance
- Genus: The Klein quartic is a compact Riemann surface of genus 3. In simpler terms, it can be visualized as a surface with three “holes”.
- Symmetry: It has the largest possible symmetry group for its genus, known as the automorphism group, which is isomorphic to ( PSL(2,7) ) (Projective Special Linear group).
Applications
- Algebraic Geometry:
- The Klein quartic serves as an example in the study of algebraic curves and their properties. Its rich symmetry makes it a useful test case for various theoretical explorations.
- Number Theory:
- The symmetries of the Klein quartic relate to the symmetries of certain modular forms and can be used to study congruences and properties of numbers.
- Hyperbolic Geometry:
- The Klein quartic is a prime example of a surface that can be studied within the framework of hyperbolic geometry, providing insights into the nature of spaces with constant negative curvature.
- Group Theory:
- The automorphism group of the Klein quartic, ( PSL(2,7) ), is a well-known simple group. Studying this group through the Klein quartic helps in understanding the structure and properties of other simple groups.
- Theoretical Physics:
- In string theory and related areas, the Klein quartic and similar structures are used to explore concepts like compactification, where additional dimensions of space are compactified on complex surfaces.
- Cryptography:
- Certain aspects of the Klein quartic and related algebraic curves are studied in the context of elliptic curve cryptography and other advanced cryptographic protocols.
Conclusion
The Klein quartic is a fascinating mathematical object with deep connections to various areas of mathematics and theoretical physics. Its rich structure and high symmetry make it an important subject of study for understanding more complex algebraic and geometric phenomena.
A Riemann surface is a one-dimensional complex manifold, which can be thought of as a shape that locally resembles the complex plane. Here’s a detailed explanation:
Definition and Basic Properties
- Complex Manifold: A Riemann surface is a complex manifold of dimension one. This means it is a space that locally looks like the complex plane ( \mathbb{C} ) and is equipped with complex coordinates.
- Charts and Atlases: Just like a smooth surface can be covered by patches (charts) that look like pieces of the Euclidean plane, a Riemann surface can be covered by charts that look like pieces of the complex plane. An atlas is a collection of such charts that cover the entire surface.
- Complex Structure: The transition maps between overlapping charts are holomorphic functions, meaning they are complex differentiable. This requirement ensures that the surface has a consistent complex structure.
Examples of Riemann Surfaces
- Complex Plane ( \mathbb{C} ): The simplest example of a Riemann surface is the complex plane itself, where each point is described by a single complex coordinate ( z ).
- Riemann Sphere: This is the complex plane plus a point at infinity, often denoted ( \mathbb{C} \cup {\infty} ) or ( \mathbb{P}^1 ). It can be visualized as the surface of a sphere where one point (the north pole) represents infinity.
- Torus: A torus can be described as a complex plane modulo a lattice of translations, resulting in a doughnut-shaped surface. It can also be seen as a quotient space ( \mathbb{C} / (\mathbb{Z} + \tau \mathbb{Z}) ), where ( \tau ) is a complex number with a positive imaginary part.
- Algebraic Curves: Solutions to polynomial equations in two complex variables, like the Klein quartic defined by ( x^3y + y^3z + z^3x = 0 ), are also Riemann surfaces. These can have more complex shapes and structures.
Importance and Applications
- Complex Analysis: Riemann surfaces provide a natural setting for studying complex functions. Many properties of complex functions, like conformal mappings, are best understood in the context of Riemann surfaces.
- Algebraic Geometry: Riemann surfaces are closely related to algebraic curves. The study of these surfaces helps in understanding the solutions to polynomial equations and their geometric properties.
- Topology: The classification of Riemann surfaces involves topological properties such as genus (the number of “holes” in the surface). This classification is crucial in various branches of mathematics and theoretical physics.
- Theoretical Physics: Riemann surfaces appear in string theory, where the shape and topology of the surfaces can affect the physical properties of strings. They are also used in the study of quantum field theory and conformal field theory.
Genus of a Riemann Surface
- The genus is a topological invariant that describes the number of “holes” in a surface. For example, a sphere has genus 0, a torus has genus 1, and a double torus has genus 2.
- Higher-genus surfaces can be constructed by connecting multiple tori.
Uniformization Theorem
- One of the central results related to Riemann surfaces is the Uniformization Theorem, which states that every simply connected Riemann surface is conformally equivalent to one of the following three:
- The complex plane ( \mathbb{C} )
- The Riemann sphere ( \mathbb{P}^1 )
- The unit disk ( \mathbb{D} )
Conclusion
Riemann surfaces are fundamental objects in complex analysis, algebraic geometry, and many areas of theoretical physics. They provide a rich structure for understanding complex functions, topological properties, and geometric shapes, making them an essential concept in modern mathematics.

Here are some concrete examples of how the Klein quartic is used in various fields:
Algebraic Geometry
- Explicit Equations: The Klein quartic can be defined explicitly by the equation ( x^3y + y^3z + z^3x = 0 ). Studying the solutions to this equation and their geometric properties provides insights into more general properties of algebraic curves.
- Moduli Space: The Klein quartic plays a role in the study of moduli spaces of curves, which are spaces that parametrize algebraic curves of a fixed genus. The high symmetry of the Klein quartic makes it a special point in these moduli spaces.
Number Theory
- Congruence Properties: The symmetries of the Klein quartic can be linked to congruences between numbers. For example, the automorphisms of the curve can be used to construct special kinds of congruences and modular forms.
- Modular Forms: The relationship between the Klein quartic and modular forms, particularly those with high levels of symmetry, helps in understanding the structure and transformation properties of these forms.
Hyperbolic Geometry
- Tilings: The Klein quartic can be visualized as a tiling of the hyperbolic plane with regular heptagons (seven-sided polygons). This tiling exhibits the maximal symmetry possible for such a surface, helping to study tiling patterns and their properties in hyperbolic space.
- Uniformization Theorem: The Klein quartic serves as an example in the study of the uniformization theorem, which states that every Riemann surface can be represented as a quotient of the hyperbolic plane by a discrete group of isometries.
Group Theory
- Simple Groups: The automorphism group of the Klein quartic, ( PSL(2,7) ), is a simple group. Studying the Klein quartic provides a concrete example of how simple groups can act on algebraic curves, shedding light on the structure and properties of these groups.
- Representation Theory: The action of the automorphism group on the Klein quartic can be used to study its representations, which are ways of expressing group elements as matrices. This helps in understanding the algebraic structure of the group.
Theoretical Physics
- String Theory: In string theory, compactification involves wrapping extra dimensions around complex surfaces like the Klein quartic. This provides a model for understanding how higher-dimensional spaces might look and behave.
- Mirror Symmetry: The Klein quartic can be used in the study of mirror symmetry, a phenomenon in string theory where two different geometric shapes yield equivalent physical theories. The rich symmetry of the Klein quartic makes it a valuable example in this context.
Cryptography
- Elliptic Curves: Certain properties of the Klein quartic and its symmetries can be generalized to elliptic curves, which are used in cryptographic protocols like elliptic curve cryptography (ECC). Understanding these properties helps in designing secure cryptographic systems.
- Advanced Cryptographic Protocols: The study of algebraic curves like the Klein quartic can lead to the development of new cryptographic protocols that rely on the complexity of solving equations on these curves.
These examples illustrate the broad and deep impact of the Klein quartic across multiple areas of mathematics and science. Its unique properties and high degree of symmetry make it a powerful tool for both theoretical exploration and practical applications.

